Emil Stoyanov's New Year's Problem, a Sequel
Introduction
On the New 2017 Year's eve a problem has been posted by Emil Stoyanov at the CutTheKnotMath facebook page, with New Year greetings. With the start of the new year, new properties of the configuration have been discovered by several people and collected into an Extra section of the page. This part of the page grew up to such an extent that when more features have been discovered by a Romanian teacher Gabriela Negutescu, I decided to put them on a separate page. This is it.
Source
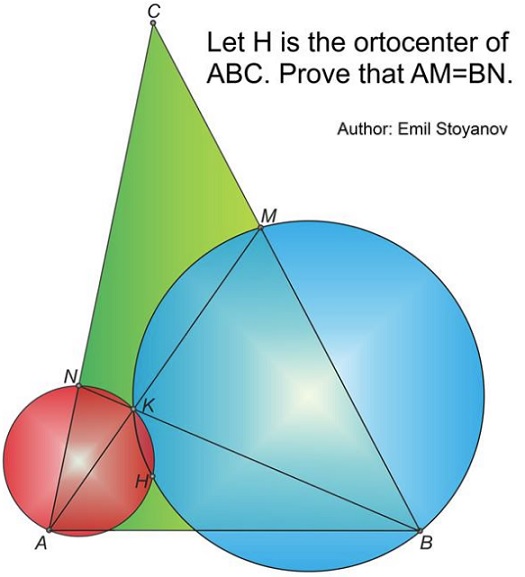
Extra's Extras 1

$\Delta MAB\,$ is isosceles, with $AM=AB\,$ and $AD\perp MB,\,$ so that $AD\,$ is the bisector of $\angle MAB\,$ and $AH\,$ the bisector of $\angle KAB.\,$ SImilarly $BH\,$ is the bisector of $\angle KBA.\,$ From these it follows that $H\,$ is the incenter of $\Delta AKB.$
Let $H_1,H_2,H_3\,$ be the projections of $H\,$ on $AB,BN,AM,\,$ respectively. We have $HH_1=HH_2=HH_3.$
In quadrilateral $NH_2HE,\,$ $\angle NH_2H+\angle NEH=180^{\circ},\,$ making $NH_2HE\,$ cyclic and implying $\angle HH_2E=\angle HNE.\,$ Together with $\angle HNE=\angle HAE,\,$ we get
(1)
$\angle HH_2E=\angle HAE.$
In quadrilateral $HH_2DB,\,$ $\angle HH_2B=\angle HDB=90^{\circ},\,$ making $HH_2DB\,$ cyclic and implying
(2)
$\angle BH_2D=\angle BHD.$
Further, $\angle BHD=\angle AHE\,(3).\,$ In $\Delta AEH,\,$ $\angle HAE+\angle AHE=90^{\circ}\,(4).\,$ From (1)-(4) we have
$\begin{align} \angle HH_2E+\angle HH_2B+\angle BH_2D &= \angle HAE+90^{\circ}+\angle BHD\\ &=90^{\circ}+\angle HAE+\angle AHE\\ &=90^{\circ}+90^{\circ}=180^{\circ}, \end{align}$
Meaning $H_2\in ED.\,$ Similarly, $H_3\in ED.\,$ It follows that $E, H_3,H_2,D\,$ are collinear.
Extra's Extras 2
The below is specifically related to the Extra 4 feature on the original page:

Since $UAHN\,$ is cyclic,
$\begin{align}\angle UAN&=\angle UHN=\angle UHA\\ &=90^{\circ}-\angle HAE=\angle C, \end{align}$
because $\Delta CDA\,$ is right. Now from $\angle UAN=\angle ACB\,$ it follows that $UA\parallel BC.\,$ Similarly, $VB\parallel AC.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574125
