How to Construct Common Tangents to Two Circles
Given circles \(A(B)\) and \(C(D)\), construct the lines tangent to the two circles.

Below is an applet that is supposed to be suggestive of the construction:
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Given circles \(A(B)\) and \(C(D)\), construct the lines tangent to the two circles.

As is often the case in mathematics, the sought construction of common tangents two to circles is reduced to a simpler construction of tangents from a point to a circle.
To see how it works, let's introduce notation \(R_c\)for the radius of circle \(c\). Assume (without loss of generality) that \(R_{(A)}\ge R_{(B)}.\) Form an auxiliary circle \((A)'\) with center \(A\) and radius \(R_{(A)}\ge R_{(B)}.\)
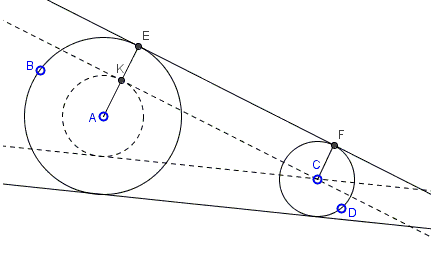
Tangents to a circle are perpendicular to the radii at the points of contact. Thus, in the diagram, if \(CK\) is tangent to \((A)'\) then \(AK\perp CK.\) If \(E\) is the intersection of \(AK\) with \(A(B)\) and \(AK||CF\), with \(F\) on \(C(D)\), then, first of all \(AE\) and \(CF\) are radii of \(A(B)\) and \(C(D),\) respectively. Also, by the construction, \(KE=CF,\) \(KE||CF,\), and the angle at \(K\) is right, making \(ACFE\) a rectangle. It follows that the radii \(AE\) and \(CF\) are perpendicular to \(EF\), implying tat the latter is tangent to both circles.
To construct the inner tangents, reduce first \(C(D)\) to a point and simultaneously expand \(A(B)\) by \(R_{C(D)}.\) The argument is about the same as before.

Several cases are possible. If the circles coincide, the number of common tangents is infinite - one per every point on the circle. If one of the circles lies entirely within the other, they have no common tangents. If they touch internally, their single common tangent can be said to play a double role. If the circles intersect, they have two outer tangents. If they touch externally, there are two outer tangents and one tangent at their common point. Otherwise, there are two outer and two inner tangents.
When two circles are tangent externally, their common tangents are found to be in an interesting relationship.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73569704
